Code
n_cases_trn <- 100
n_cases_test <- 1000
n_x <- 20
covs_x <- 50
vars_x <- 100
b_x <- rep(1, n_x) # one unit change in y for 1 unit change in x
y_error <- 1006 Regularization and Penalized Models
6.1 Learning Objectives
- Subsetting approaches: Forward, Backward, Best Subset (covered in reading only)
- Cost and Loss functions
- What are they and how are they used
- What are the specific formulas for linear model, logistic regression, and variants of glmnet (ridge, LASSO, full elasticnet)
- What is regularization
- What are its benefits?
- What are its costs?
- How does lambda affect bias-variance trade-off in glmnet
- What does alpha do?
- Feature engineering approaches for dimensionality reduction: PCA (covered in reading only)
- Other algorithms that do feature selection/dimensionality reduction: PCR and PLS (covered in reading only)
- Contrasts of PCA, PCR, PLS, and glmnet/LASSO for dimensionality reduction (covered in reading only)
6.2 Introduction to Penalized/Regularized Statistical Algorithms
6.2.1 Overview
Complex (e.g., flexible) models increase the chance of overfitting to the training set. This leads to:
- Poor prediction
- Burdensome prediction models for implementation (need to measure lots of predictors)
- Low power to test hypothesis about predictor effects
Complex models are difficult to interpret
Regularization is technique that:
- Reduces overfitting
- Allows for p >> n (!!!)
- May yield more interpretable models (LASSO, Elastic Net)
- May reduce implementation burden (LASSO, Elastic Net)
Regularization does this by applying a penalty to the parametric model coefficients (parameter estimates)
- This constrains/shrinks these coefficients to yield a simpler/less overfit model
- Some types of penalties shrink the coefficients to zero (feature selection)
We will consider three approaches to regularization
- L2 (Ridge)
- L1 (LASSO)
- Elastic net
These approaches are available for both regression and classification problems and for a variety of parametric statistical algorithms
6.2.2 Cost functions
To understand regularization, we need to first explicitly consider loss/cost functions for the parametric statistical models we have been using.
A loss function quantifies the error between a single predicted and observed outcome within some statistical model.
A cost function is simply the aggregate of the loss across all observations in the training sample.
Optimization procedures (least squares, maximum likelihood, gradient descent) seek to determine a set of parameter estimates that minimize some specific cost function for the training sample.
The cost function for the linear model is the mean squared error (squared loss):
\(\frac{1}{n}\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}\)
No constraints or penalties are placed on the parameter estimates (\(\beta_k\))
They can take on any values with the only goal to minimize the MSE in the training sample
The cost function for logistic regression is log loss:
\(\frac{1}{n}\sum_{i = 1}^{n} -Y_ilog(\hat{Y_i}) - (1-Y_i)log(1-\hat{Y_i})\)
where \(Y_i\) is coded 0,1 and \(\hat{Y_i}\) is the predicted probability that Y = 1
Again, no constraints or penalties are placed on the parameter estimates (\(\beta_k\))
They can take on any values with the only goal to minimize the sum of the log loss in the training sample
6.3 Intuitions about Penalized Cost Functions and Regularization
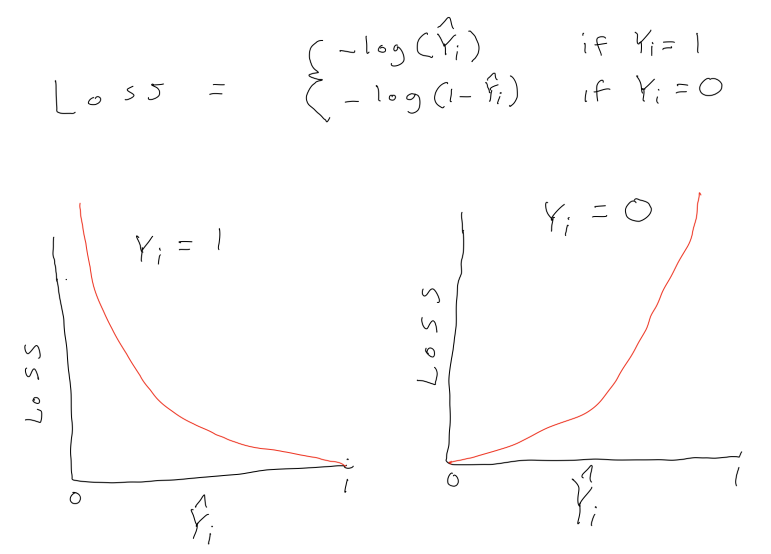
This is an example from a series of wonderfully clear lectures in a machine learning course by Andrew Ng in Coursera.
Lets imagine a training set:
- House sale price predicted by house size
- True DGP is quadratic. Diminishing increase in sale price as size increases
- N = 5 in training set
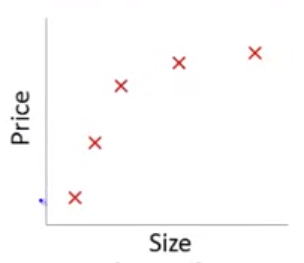
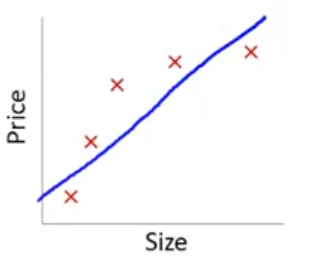
If we fit a linear model with size as the only feature…
\(\hat{sale\_price_i} = \beta_0 + \beta_1 * size\)
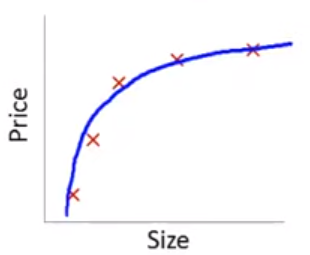
In this training set, we might get the model below (in blue)
This is a biased model (predicts too high for low and high house sizes; predicts too low for moderate size houses)
If we took this model to new data from the same quadratic DGP, it would clearly not predict very well
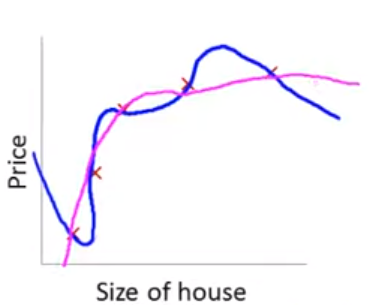
Lets consider the other extreme
- If we fit a 4th order polynomial model using size…
- \(\hat{sale\_price_i} = \beta_0 + \beta_1 * size + \beta_2 * size^2 + \beta_3 * size^3 + \beta_4 * size^4\)
- In this training set, we would get the model below (in blue)
- This is model is overfit to this training set. It would not predict well in new data from the same quadratic DGP
- Also, the model would have high variance (if we estimated the parameters in another N = 5 training set, they would be very different)
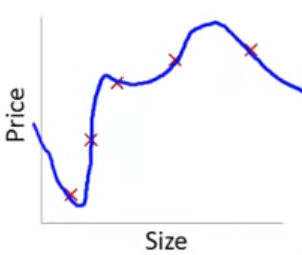
This problem with overfitting and variance isn’t limited to polynomial regression.
We would have the same problem (perfect fit in training with poor fit in new val data) if we predicted housing prices with many features when the training N = 5. e.g.,
\(\hat{sale\_price_i} = \beta_0 + \beta_1 * size + \beta_2 * year\_built + \beta_3 * num\_garages + \beta_4 * quality\)
Obviously, the correct model to fit is a second order polynomial model with size
- \(\hat{sale\_price_i} = \beta_0 + \beta_1 * size + \beta_2 * size^2\)
- But we couldn’t know this with real data because we wouldn’t know the underlying DGP
- When we don’t know the underlying DGP, we need to be able to consider potentially complex models with many features in some way that diminishes the potential problem with overfitting/model variance
What if we still fit a fourth order polynomial but changed the cost function to penalize the absolute value of \(\beta_3\) and \(\beta_4\) parameter estimates?
Typical cost based on MSE/squared loss:
- \(\frac{1}{n}\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}\)
Our new cost function:
- \([\frac{1}{n}\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [1000 * \beta_3 + 1000 * \beta_4]\)
\([\frac{1}{n}\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [1000 * \beta_3 + 1000 * \beta_4]\)
The only way to make the value of this new cost function small is to make \(\beta_3\) and \(\beta_4\) small
If we made the penalty applied to \(\beta_3\) and \(\beta_4\) large (e.g., 1000 as above), we will end up with the parameter estimates for these two features at approximately 0.
With a sufficient penalty applied, their parameter estimates will only change from zero to the degree that these changes accounted for a large enough drop in MSE to offset this penalty in the overall aggregate cost function.
\([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + 1000 * \beta_3 + 1000 * \beta_4\)
- With this penalty in place, our final model might shift from the blue model to the pink model below. The pink model is mostly quadratic but with a few extra “wiggles” if \(\beta_3\) and \(\beta_4\) are not exactly 0.
Of course, we don’t typically know in advance which parameter estimates to penalize.
- Instead, we apply some penalty to all the parameter estimates (except \(\beta_0\))
- This shrinks the parameter estimates for all the features to some degree
- However, features that do reduce MSE meaningfully will be “worth” including with non-zero parameter estimates
- You can also control the shrinkage by controlling the size of the penalty
In general, regularization produces models that:
- Are simpler (e.g. smoother, smaller coefficients/parameter estimates)
- Are less prone to overfitting
- Allow for models with p >> n
- Are sometimes more interpretable (LASSO, Elastic Net)
These benefits are provided by the introduction of some bias into the parameter estimates
This allows for a bias-variance trade-off where some bias is introduced for a big reduction in variance of model fit
We will now consider three regularization approaches that introduce different types of penalties to shrink the parameter estimates
- L2 (Ridge)
- L1 (LASSO)
- Elastic net
These approaches are available for both regression and classification problems and for a variety of parametric statistical algorithms
A fourth common regularized classification model (also sometimes used for regression) is the support vector machine (not covered in class but commonly used as well and easy to understand with this foundation)
Each of these approaches uses a different specific penalty, which has implications for how the model performs in different settings
6.4 Ridge Regression
The cost function for Ridge Regression is:
- \(\frac{1}{n}([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [\:\lambda\sum_{j = 1}^{p} \beta_j^{2}\:])\)
It has two components:
- Inside the left brackets is the SSE from linear regression
- Inside the right brackets is the Ridge penalty.
This penalty:
- Includes the sum of the squared parameter estimates (excluding \(\beta_0\)). Squaring removes the sign of these parameter estimates.
- This sum is multiplied by \(\lambda\), a hyperparameter in Ridge regression. Lambda allows us to tune the size of the penalty.
- This is an application of the L2 norm (matrix algebra) to the vector of parameter estimates
\(\frac{1}{n}([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [\:\lambda\sum_{j = 1}^{p} \beta_j^{2}\:])\)
As lambda increases, the model becomes less flexible b/c its parameter estimates become constrained/shrunk. This will increase bias but decrease variance for model performance.
\(\frac{1}{n}([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [\:\lambda\sum_{j = 1}^{p} \beta_j^{2}\:])\)
The OLS regression is a special case where lambda = 0 (i.e., no penalty is applied).
This is the most flexible. It is unbiased but with higher variance than for non-zero values of lambda
Lets compare Ridge regression to OLS (ordinary least squares with squared loss cost function) linear regression
Ridge parameter estimates are biased but have lower variance (smaller SE) than OLS
Ridge may predict better in new data
- This depends on the value of \(\lambda\) selected and its impact on bias-variance trade-off in Ridge regression vs. OLS
- There does exist a value of \(\lambda\) for which Ridge predicts better than OLS in new data
Ridge regression (but not OLS) allows for p > (or even >>) than n
Ridge regression (but not OLS) accommodates highly correlated (or even perfectly multi-collinear) features
OLS (but not Ridge regression) is scale invariant
- You should scale (mean and standard deviation correct) features for use with Ridge regression
\(\frac{1}{n}([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [\:\lambda\sum_{j = 1}^{p} \beta_j^{2}\:])\)
Features with bigger SDs will have smaller parameter estimates. Therefore they will be less affected by the penalty.
Unless the features are on the same scale to start, you should standardize them for all applications (regression and classification) of Ridge (and also LASSO and elastic net). You can handle this during feature engineering in the recipe.
6.5 LASSO Regression
LASSO is an acronym for Least Absolute Shrinkage and Selection Operator
The cost function for LASSO Regression is:
- \(\frac{1}{n}([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [\:\lambda\sum_{j = 1}^{p} |\beta_j|\:])\)
It has two components:
- Inside the left brackets is the SSE from linear regression
- Inside the right brackets is the LASSO penalty.
This penalty:
Includes the sum of the absolute value of the parameter estimates (excluding \(\beta_0\)). The absolute value removes the sign of these parameter estimates.
This sum is multiplied by \(\lambda\), a hyperparameter in LASSO regression. Lambda allows us to tune the size of the penalty.
This is an application of the L1 norm to the vector of parameter estimates
6.5.1 LASSO vs. Ridge Comparison
With respect to the parameter estimates:
LASSO yields sparse solution (some parameter estimates set to exactly zero)
Ridge tends to retain all features (parameter estimates don’t get set to exactly zero)
LASSO selects one feature among correlated group and sets others to zero
Ridge shrinks all parameter estimates for correlated features
Ridge tends to outperform LASSO wrt prediction in new data. There are cases where LASSO can predict better (most features have zero effect and only a few are non-zero) but even in those cases, Ridge is competitive.
6.5.2 Advantages of LASSO
Does feature selection (sets parameter estimates to exactly 0)
- Yields a sparse solution
- Sparse model is more interpretable?
- Sparse model is easier to implement? (fewer features included so don’t need to measure as many predictors)
More robust to outliers (similar to LAD vs. OLS)
Tends to do better when there are a small number of robust features and the others are close to zero or zero
6.5.3 Advantages of Ridge
Computationally superior (closed form solution vs. iterative; Only one solution to minimize the cost function)
More robust to measurement error in features (remember no measurement error is an assumption for unbiased estimates in OLS regression)
Tends to do better when there are many features with large (and comparable) effects (i.e., most features are related to the outcome)
6.6 Elastic Net Regression
The Elastic Net blends the L1 and L2 penalties to obtain the benefits of each of those approaches.
We will use the implementation of the Elastic Net in glmnet in R.
You can also read additional introductory documentation for this package
In the Gaussian regression context, the Elastic Net cost function is:
- \(\frac{1}{n}([\sum_{i = 1}^{n} (Y_i - \hat{Y_i})^{2}] + [\:\lambda (\alpha\sum_{j = 1}^{p} |\beta_j| + (1-\alpha)\sum_{j = 1}^{p} \beta_j^{2})\:])\)
This model has two hyper-parameters
- \(\lambda\) controls the degree of regularization as before
- \(\alpha\) is a “mixing” parameter that blends the degree of L1 and L2 contributions to the aggregate penalty. (Proportion of LASSO penalty)
- \(\alpha\) = 1 results in the LASSO model
- \(\alpha\) = 0 results in the Ridge model
- Intermediate values for \(\alpha\) blend these penalties together proportionally to include more or less LASSO penalty
As before (e.g., KNN), best values of \(\lambda\) (and \(\alpha\)) can be selected using resampling using tune_grid()
The grid needs to have crossed values of both penalty (\(lambda\)) and mixture (\(alpha\)) for glmnet
- Can use
expand_grid() - Only penalty is needed in grid if fitting a Ridge or LASSO model.
6.7 Empirical Example 1: Many “good” but correlated predictors
For the first example, we will simulate data with:
- Many correlated predictors
- All related to outcome
- Get a small training sample
- Get a big test sample (for more precise estimate of model performance)
First we set the predictors for our simulation
Then we draw samples from population
Code
set.seed(12345)
mu <- rep(0, n_x) # means for all variables = 0
sigma <- matrix(covs_x, nrow = n_x, ncol = n_x)
diag(sigma) <- vars_x
sigma [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
[1,] 100 50 50 50 50 50 50 50 50 50 50 50 50
[2,] 50 100 50 50 50 50 50 50 50 50 50 50 50
[3,] 50 50 100 50 50 50 50 50 50 50 50 50 50
[4,] 50 50 50 100 50 50 50 50 50 50 50 50 50
[5,] 50 50 50 50 100 50 50 50 50 50 50 50 50
[6,] 50 50 50 50 50 100 50 50 50 50 50 50 50
[7,] 50 50 50 50 50 50 100 50 50 50 50 50 50
[8,] 50 50 50 50 50 50 50 100 50 50 50 50 50
[9,] 50 50 50 50 50 50 50 50 100 50 50 50 50
[10,] 50 50 50 50 50 50 50 50 50 100 50 50 50
[11,] 50 50 50 50 50 50 50 50 50 50 100 50 50
[12,] 50 50 50 50 50 50 50 50 50 50 50 100 50
[13,] 50 50 50 50 50 50 50 50 50 50 50 50 100
[14,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[15,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[16,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[17,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[18,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[19,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[20,] 50 50 50 50 50 50 50 50 50 50 50 50 50
[,14] [,15] [,16] [,17] [,18] [,19] [,20]
[1,] 50 50 50 50 50 50 50
[2,] 50 50 50 50 50 50 50
[3,] 50 50 50 50 50 50 50
[4,] 50 50 50 50 50 50 50
[5,] 50 50 50 50 50 50 50
[6,] 50 50 50 50 50 50 50
[7,] 50 50 50 50 50 50 50
[8,] 50 50 50 50 50 50 50
[9,] 50 50 50 50 50 50 50
[10,] 50 50 50 50 50 50 50
[11,] 50 50 50 50 50 50 50
[12,] 50 50 50 50 50 50 50
[13,] 50 50 50 50 50 50 50
[14,] 100 50 50 50 50 50 50
[15,] 50 100 50 50 50 50 50
[16,] 50 50 100 50 50 50 50
[17,] 50 50 50 100 50 50 50
[18,] 50 50 50 50 100 50 50
[19,] 50 50 50 50 50 100 50
[20,] 50 50 50 50 50 50 100Code
x <- MASS::mvrnorm(n = n_cases_trn, mu, sigma) |>
magrittr::set_colnames(str_c("x_", 1:n_x)) |>
as_tibble()
data_trn_1 <- x |>
mutate(y = rowSums(t(t(x)*b_x)) + rnorm(n_cases_trn, 0, y_error)) |>
glimpse()Rows: 100
Columns: 21
$ x_1 <dbl> -7.4799044, 1.0236917, 6.7326934, -14.9063964, 0.8889487, 6.11951…
$ x_2 <dbl> -4.382765, -16.434199, -1.959195, 2.370728, -5.953006, 12.740186,…
$ x_3 <dbl> -1.3926483, -11.8268783, 1.9367593, 6.3597281, -4.7341473, 13.669…
$ x_4 <dbl> -1.4098139, -18.1013510, -0.4859097, -10.1016905, 4.9501196, 21.1…
$ x_5 <dbl> -11.32152449, -6.57272989, 6.99237521, -4.05418224, -9.28203264, …
$ x_6 <dbl> 0.4287849, 1.0753238, 7.7437722, 3.2533250, 4.9400340, 25.6213841…
$ x_7 <dbl> -6.0659342, -2.3248026, -4.2596876, 1.5548678, -8.3378011, 18.483…
$ x_8 <dbl> -11.7704021, -2.7225251, -2.9738809, 11.7014682, 4.7353163, 13.29…
$ x_9 <dbl> -17.65256942, -16.75121020, 7.42850231, 2.93173355, 15.15289724, …
$ x_10 <dbl> -3.7916335, -3.5774760, 4.3791349, 4.1647748, 1.8069956, 13.21176…
$ x_11 <dbl> 1.7944916, 6.8024759, -5.6288959, 7.8606019, -11.4396013, 12.8486…
$ x_12 <dbl> 7.2748185, 1.1123695, 5.4570129, 7.7298625, -8.4277385, 9.1001513…
$ x_13 <dbl> 3.9636299, 1.0714662, 6.4823620, 9.2692615, -0.2841161, 19.649099…
$ x_14 <dbl> -12.4510389, -19.6153036, -7.2578101, 9.0097406, -3.8630757, -0.9…
$ x_15 <dbl> -18.423674, -4.868512, -4.172538, 13.451919, -8.647879, 18.845043…
$ x_16 <dbl> -11.53843545, 0.26737312, -2.75900928, -0.03913761, -12.88983878,…
$ x_17 <dbl> 3.7450353, -0.4135728, -10.8964534, 3.5617282, -16.3498259, 12.86…
$ x_18 <dbl> -6.774703, -14.686612, 1.777447, 13.867454, -10.362955, 15.853674…
$ x_19 <dbl> 3.9091399, 0.1744112, 11.4781208, 2.2775369, -6.0500447, 8.658232…
$ x_20 <dbl> 8.487960, 3.556668, -4.175244, -4.545339, -13.653683, 9.542350, -…
$ y <dbl> -145.635298, 4.810920, -41.803024, 175.580620, 52.932735, 267.112…Code
x <- MASS::mvrnorm(n = n_cases_test, mu, sigma) |>
magrittr::set_colnames(str_c("x_", 1:n_x)) |>
as_tibble()
data_test_1 <- x |>
mutate(y = rowSums(t(t(x)*b_x)) + rnorm(n_cases_test, 0, y_error))Set up a tibble to track model performance in train and test sets
- We are using test to repeatedly to get rigorous held-out performance separate from model selection process.
- Just for our understanding
- We would not choose a model configuration based on test set error
Code
error_ex1 <- tibble(model = character(),
rmse_trn = numeric(),
rmse_test = numeric()) |>
glimpse()Rows: 0
Columns: 3
$ model <chr>
$ rmse_trn <dbl>
$ rmse_test <dbl> 6.7.1 Fit a standard (OLS) linear regression
Fit the linear model
- No feature engineering needed. Can use raw predictors as features
- No resampling needed b/c there are no hyperparameters
Code
fit_lm_1 <-
linear_reg() |>
set_engine("lm") |>
fit(y ~ ., data = data_trn_1)
fit_lm_1 |>
tidy() |>
print(n = 21)# A tibble: 21 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -5.22 12.0 -0.436 0.664
2 x_1 -1.26 1.71 -0.736 0.464
3 x_2 -0.112 1.53 -0.0732 0.942
4 x_3 0.780 1.43 0.545 0.588
5 x_4 0.970 1.54 0.632 0.529
6 x_5 -0.327 1.52 -0.215 0.830
7 x_6 -0.325 1.67 -0.195 0.846
8 x_7 0.896 1.75 0.512 0.610
9 x_8 1.83 1.69 1.08 0.282
10 x_9 3.64 1.63 2.24 0.0282
11 x_10 3.84 1.55 2.47 0.0155
12 x_11 3.11 1.78 1.75 0.0845
13 x_12 0.592 1.78 0.332 0.741
14 x_13 0.108 1.61 0.0669 0.947
15 x_14 1.15 1.46 0.787 0.434
16 x_15 -1.60 1.73 -0.922 0.359
17 x_16 1.75 1.87 0.935 0.353
18 x_17 3.17 1.64 1.93 0.0569
19 x_18 1.35 1.67 0.811 0.420
20 x_19 1.53 1.51 1.01 0.315
21 x_20 -0.908 1.57 -0.580 0.564 Irreducible error was set by y_error (100)
- Overfit to train
- Much worse in test
Code
rmse_vec(truth = data_trn_1$y,
estimate = predict(fit_lm_1, data_trn_1)$.pred)[1] 91.86214Code
rmse_vec(truth = data_test_1$y,
estimate = predict(fit_lm_1, data_test_1)$.pred)[1] 112.32086.7.2 Fit LASSO
LASSO, Ridge, and glmnet all need features on same scale to apply penalty consistently
- Use
step_normalize(). This sets mean = 0, sd = 1 (NOTE: Bad name as it does NOT change shape of distribution!) - Can use same recipe for LASSO, Ridge, and glmnet
- Can use same train and test feature matrices as well
Code
rec_1 <- recipe(y ~ ., data = data_trn_1) |>
step_normalize(all_predictors())
rec_prep_1 <- rec_1 |>
prep(data_trn_1)
feat_trn_1 <- rec_prep_1 |>
bake(NULL)
feat_test_1 <- rec_prep_1 |>
bake(data_test_1)Set up splits for resampling for tuning hyperparameters
- Use bootstrap for more precise estimation (even if more biased). Good for selection
- Can use same bootstrap splits for LASSO, Ridge, and glmnet
Code
set.seed(20140102)
splits_boot_1 <- data_trn_1 |>
bootstraps(times = 100, strata = "y") Now onto the LASSO….
We need to tune \(\lambda\) (tidymodels calls this penalty)
- \(\alpha\) = 1 (tidymodels calls this
mixture) - Set up grid with exponential values for
penalty glmnetuses warm starts so can fit lots of values for \(\lambda\) quickly- Could also use
cv.glmnet()directly inglmnetpackage to find good values. Seeget_lamdas()in fun_modeling.R
Code
grid_lasso <- expand_grid(penalty = exp(seq(-4, 4, length.out = 500)))Code
fits_lasso_1 <- xfun::cache_rds(
expr = {
linear_reg(penalty = tune(),
mixture = 1) |>
set_engine("glmnet") |>
tune_grid(preprocessor = rec_1,
resamples = splits_boot_1,
grid = grid_lasso,
metrics = metric_set(rmse))
},
rerun = rerun_setting,
dir = "cache/006/",
file = "fits_lasso_1")Evaluate model performance in validation sets (OOB)
Make sure that you have hit a clear minimum (bottom of U or at least an asymptote)
Code
plot_hyperparameters(fits_lasso_1, hp1 = "penalty", metric = "rmse")
Fit best configuration (i.e., best lambda) to full train set
- Use
select_best() - Don’t forget to indicate which column (\(penalty\))
Code
fit_lasso_1 <-
linear_reg(penalty = select_best(fits_lasso_1)$penalty,
mixture = 1) |>
set_engine("glmnet") |>
fit(y ~ ., data = feat_trn_1)Warning in select_best(fits_lasso_1): No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.We can now use tidy() to look at the LASSO parameter estimates
tidy()usesMatrixpackage, which has conflicts withtidyr. Load the package without those conflicting functions
Code
library(Matrix, exclude = c("expand", "pack", "unpack"))Now call tidy()
- Notice that LASSO sets some \(\beta\) to 0 even though none are 0 in DGP
- LASSO is not great at reproducing the DGP!
Code
fit_lasso_1 |>
tidy() |>
print(n = 21)Loaded glmnet 4.1-8# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) -41.2 10.8
2 x_1 0 10.8
3 x_2 0 10.8
4 x_3 4.89 10.8
5 x_4 6.63 10.8
6 x_5 0 10.8
7 x_6 0 10.8
8 x_7 10.7 10.8
9 x_8 9.46 10.8
10 x_9 34.6 10.8
11 x_10 32.0 10.8
12 x_11 25.4 10.8
13 x_12 3.23 10.8
14 x_13 0.681 10.8
15 x_14 8.38 10.8
16 x_15 0 10.8
17 x_16 14.5 10.8
18 x_17 22.9 10.8
19 x_18 13.4 10.8
20 x_19 6.83 10.8
21 x_20 0 10.8Irreducible error was set by y_error (100)
- Somewhat overfit to train
- Somewhat better in test
Code
(error_ex1 <- error_ex1 |>
bind_rows(tibble(model = "LASSO model",
rmse_trn = rmse_vec(truth = feat_trn_1$y,
estimate = predict(fit_lasso_1,
feat_trn_1)$.pred),
rmse_test = rmse_vec(truth = feat_test_1$y,
estimate = predict(fit_lasso_1,
feat_test_1)$.pred))))# A tibble: 2 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 91.9 112.
2 LASSO model 94.0 108.6.7.3 Fit Ridge
Fit Ridge algorithm
- Tune \(\lambda\) (
penalty) - May need to experiment to get right range of values for lambda
- \(\alpha\) = 0 (
mixture) - Evaluate model configurations in OOB validation sets
Code
grid_ridge <- expand_grid(penalty = exp(seq(-1, 7, length.out = 500)))Code
grid_ridge <- expand_grid(penalty = exp(seq(-1, 7, length.out = 500)))Code
fits_ridge_1 <- xfun::cache_rds(
expr = {
linear_reg(penalty = tune(),
mixture = 0) |>
set_engine("glmnet") |>
tune_grid(preprocessor = rec_1,
resamples = splits_boot_1,
grid = grid_ridge,
metrics = metric_set(rmse))
},
rerun = rerun_setting,
dir = "cache/006/",
file = "fits_ridge_1")Review hyperparameter plot
Code
plot_hyperparameters(fits_ridge_1, hp1 = "penalty", metric = "rmse")
Fit best model configuration (i.e., best lambda) in full train set
- Notice that no \(\beta\) are exactly 0
- Why are parameter estimates not near 1 for LASSO and Ridge?
Code
fit_ridge_1 <-
linear_reg(penalty = select_best(fits_ridge_1)$penalty,
mixture = 0) |>
set_engine("glmnet") |>
fit(y ~ ., data = feat_trn_1)Warning in select_best(fits_ridge_1): No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.Code
fit_ridge_1 |>
tidy() |>
print(n = 21)# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) -41.2 276.
2 x_1 5.99 276.
3 x_2 6.87 276.
4 x_3 9.14 276.
5 x_4 9.00 276.
6 x_5 5.24 276.
7 x_6 8.53 276.
8 x_7 11.2 276.
9 x_8 9.12 276.
10 x_9 14.0 276.
11 x_10 14.5 276.
12 x_11 13.5 276.
13 x_12 7.14 276.
14 x_13 7.97 276.
15 x_14 10.2 276.
16 x_15 7.47 276.
17 x_16 10.3 276.
18 x_17 12.5 276.
19 x_18 11.8 276.
20 x_19 7.70 276.
21 x_20 4.57 276.Irreducible error was set by y_error (100)
- Much less overfit to train
- Still not bad in test
Code
(error_ex1 <- error_ex1 |>
bind_rows(tibble(model = "Ridge model",
rmse_trn = rmse_vec(truth = feat_trn_1$y,
estimate = predict(fit_ridge_1,
feat_trn_1)$.pred),
rmse_test = rmse_vec(truth = feat_test_1$y,
estimate = predict(fit_ridge_1,
feat_test_1)$.pred))))# A tibble: 3 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 91.9 112.
2 LASSO model 94.0 108.
3 Ridge model 98.5 104.6.7.4 Fit glmnet
Now we need to tune both
- \(\lambda\) (
penalty) - \(\alpha\) (
mixture) - Typical to only evaluate a small number of \(alpha\)
- Warm starts across \(\lambda\)
Code
grid_glmnet <- expand_grid(penalty = exp(seq(-1, 7, length.out = 500)),
mixture = seq(0, 1, length.out = 6))Code
fits_glmnet_1 <- xfun::cache_rds(
expr = {
linear_reg(penalty = tune(),
mixture = tune()) |>
set_engine("glmnet") |>
tune_grid(preprocessor = rec_1,
resamples = splits_boot_1,
grid = grid_glmnet,
metrics = metric_set(rmse))
},
rerun = rerun_setting,
dir = "cache/006/",
file = "fits_glmnet_1")Code
plot_hyperparameters(fits_glmnet_1, hp1 = "penalty", hp2 = "mixture", metric = "rmse")
Fit best configuration in full train set
- Can use
select_best()for both hyperparameters, separately - Ridge was best (but cool that glmnet could determine that empirically!)
Code
select_best(fits_glmnet_1)Warning in select_best(fits_glmnet_1): No value of `metric` was given; "rmse"
will be used.# A tibble: 1 × 3
penalty mixture .config
<dbl> <dbl> <chr>
1 276. 0 Preprocessor1_Model0414Code
fit_glmnet_1 <-
linear_reg(penalty = select_best(fits_glmnet_1)$penalty,
mixture = select_best(fits_glmnet_1)$mixture) |>
set_engine("glmnet") |>
fit(y ~ ., data = feat_trn_1)Warning in select_best(fits_glmnet_1): No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.Code
fit_glmnet_1 |>
tidy() |>
print(n = 21)# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) -41.2 276.
2 x_1 5.99 276.
3 x_2 6.87 276.
4 x_3 9.14 276.
5 x_4 9.00 276.
6 x_5 5.24 276.
7 x_6 8.53 276.
8 x_7 11.2 276.
9 x_8 9.12 276.
10 x_9 14.0 276.
11 x_10 14.5 276.
12 x_11 13.5 276.
13 x_12 7.14 276.
14 x_13 7.97 276.
15 x_14 10.2 276.
16 x_15 7.47 276.
17 x_16 10.3 276.
18 x_17 12.5 276.
19 x_18 11.8 276.
20 x_19 7.70 276.
21 x_20 4.57 276.A final comparison of training and test error for the four statistical algorithms
Code
(error_ex1 <- error_ex1 |>
bind_rows(tibble(model = "glmnet model",
rmse_trn = rmse_vec(truth = feat_trn_1$y,
estimate = predict(fit_glmnet_1,
feat_trn_1)$.pred),
rmse_test = rmse_vec(truth = feat_test_1$y,
estimate = predict(fit_glmnet_1,
feat_test_1)$.pred))))Warning in select_best(fits_glmnet_1): No value of `metric` was given; "rmse" will be used.
No value of `metric` was given; "rmse" will be used.# A tibble: 4 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 91.9 112.
2 LASSO model 94.0 108.
3 Ridge model 98.5 104.
4 glmnet model 98.5 104.6.8 Empirical Example 2: Good and Zero Predictors
For the second example, we will simulate data with:
- Two sets of correlated predictors
- First (smaller) set related to outcome (5 predictors)
- Second (larger) set unrelated to outcome (15 predictors)
- Get a small training sample
- Get a big test sample (for more precise estimates of performance of our model configurations)
Set up simulation parameters
Code
n_cases_trn <- 100
n_cases_test <- 1000
n_x <- 20
covs_x <- 50
vars_x <- 100
b_x <- c(rep(1,5),rep(0, 15))
y_error <- 100Code
mu <- rep(0, n_x)
sigma <- matrix(0, nrow = n_x, ncol = n_x)
for (i in 1:(n_x/2)){
for(j in 1:(n_x/2)){
sigma[i, j] <- covs_x
}
}
for (i in (n_x/2 + 1):n_x){
for(j in (n_x/2 + 1):n_x){
sigma[i, j] <- covs_x
}
}
diag(sigma) <- vars_x Simulate predictors and Y
Code
set.seed(2468)
x <- MASS::mvrnorm(n = n_cases_trn, mu, sigma) |>
magrittr::set_colnames(str_c("x_", 1:n_x)) |>
as_tibble()
data_trn_2 <- x |>
mutate(y = rowSums(t(t(x)*b_x)) + rnorm(n_cases_trn, 0, y_error)) |>
glimpse()Rows: 100
Columns: 21
$ x_1 <dbl> 6.6120448, -2.4315795, 10.0284465, 2.8880849, 0.6879733, 5.733069…
$ x_2 <dbl> 6.732135, -6.886575, 4.037737, -2.108035, -10.401328, 17.655429, …
$ x_3 <dbl> -7.9084791, -0.9541707, 1.9668472, -15.9822168, -3.7921834, 9.583…
$ x_4 <dbl> -1.3333051, 10.5841591, 1.0329146, -5.8848456, 5.8751565, 17.9547…
$ x_5 <dbl> 5.4258194, 18.1754493, 18.3107759, 4.2999158, -12.0440144, 18.238…
$ x_6 <dbl> -4.3345960, 6.2063944, -9.6829079, -2.3638247, -11.4994761, 16.97…
$ x_7 <dbl> 13.377810, 12.761476, 3.364706, -7.047563, -9.452121, -3.063861, …
$ x_8 <dbl> 4.9863053, -10.0216563, 6.0416675, -9.6087385, -5.2677671, 18.807…
$ x_9 <dbl> -11.2654331, 0.3969312, 4.5089003, 6.2910046, -5.5706542, 6.30376…
$ x_10 <dbl> -5.3243680, -4.1584832, 16.4302778, -4.5227897, -0.5759885, 12.27…
$ x_11 <dbl> -2.8717748, -15.9527089, -8.4020651, -21.4067819, -5.1716587, -1.…
$ x_12 <dbl> -0.8255710, -13.9063481, -7.8553560, -15.6174041, -0.2032351, -0.…
$ x_13 <dbl> -5.0226487, 0.2423470, -13.4792413, -17.7322866, -4.2641882, -13.…
$ x_14 <dbl> 1.6697344, -9.7472781, 1.9116596, -14.2383036, 3.4108820, -7.1857…
$ x_15 <dbl> -4.4078587, -17.3549677, -13.3750642, -6.3436646, -14.4783016, -1…
$ x_16 <dbl> -12.5987264, 3.0650253, -10.1369743, -15.4306537, -16.8116483, -7…
$ x_17 <dbl> 10.0679662, -16.2680745, -7.8039992, -30.4310419, -7.8560756, -0.…
$ x_18 <dbl> 4.9402996, -15.4777909, 0.5120623, -24.0317505, -2.8721223, 0.461…
$ x_19 <dbl> 3.90266477, -18.02732385, 0.09474399, -21.39430406, -11.94936843,…
$ x_20 <dbl> 5.4561394, -3.4090854, -0.3550752, -11.9522175, -5.2609615, 2.381…
$ y <dbl> -92.38562, 64.57490, 67.80447, 32.97353, 177.86063, 50.00875, 68.…Code
x <- MASS::mvrnorm(n = n_cases_test, mu, sigma) |>
magrittr::set_colnames(str_c("x_", 1:n_x)) |>
as_tibble()
data_test_2 <- x |>
mutate(y = rowSums(t(t(x)*b_x)) + rnorm(n_cases_test, 0, y_error)) |>
glimpse()Rows: 1,000
Columns: 21
$ x_1 <dbl> -19.3260095, -5.3623506, -16.9255899, 5.5493174, 14.9965119, -11.…
$ x_2 <dbl> -3.7042124, 0.1290587, -3.0372145, 9.2876528, 12.3956629, -7.8307…
$ x_3 <dbl> -7.79209805, 18.25340113, 0.06833241, -2.27459711, 8.76517873, 9.…
$ x_4 <dbl> -3.3334124, 12.2829002, 3.9338672, -3.9389029, 5.2878331, -2.1167…
$ x_5 <dbl> -34.9426303, 9.2574023, -3.6417173, -5.9916743, 10.4261807, 1.655…
$ x_6 <dbl> -0.001829374, 20.600024213, 0.173148730, 6.104400301, 8.269919307…
$ x_7 <dbl> -1.4374735, 7.5405424, 6.5958816, -5.4467627, 15.0439131, 1.45756…
$ x_8 <dbl> -15.5100796, -4.5944480, 3.8149838, 11.9367657, 11.9002354, 5.760…
$ x_9 <dbl> -14.2491503, -2.1829725, 8.8566042, 4.9237162, -1.0992521, -6.144…
$ x_10 <dbl> -9.4656790, 15.3363435, 16.4882579, 6.1347801, 7.1040896, 19.3482…
$ x_11 <dbl> -3.6565433, 4.8599310, 1.5807573, -2.0951752, 3.4182659, 8.555763…
$ x_12 <dbl> 0.2197692, -1.4002588, 15.6415398, 2.4429828, 10.3908169, 15.7459…
$ x_13 <dbl> -0.4834889, 14.4404582, -6.1966844, 2.2812604, -0.6109369, 14.888…
$ x_14 <dbl> 2.2369810, 23.6286165, 14.3772218, 4.5313060, 7.4540744, 11.28109…
$ x_15 <dbl> 12.2165650, 2.8590601, 9.6320309, -0.1679529, -1.0693068, 6.59127…
$ x_16 <dbl> -1.1872969, -4.9773499, 2.9446327, 6.4909150, 3.8271113, 7.574543…
$ x_17 <dbl> 23.2758817, 5.1783142, -5.7455295, 10.4846644, 11.1625519, -5.491…
$ x_18 <dbl> 5.26704690, 14.01330775, 15.70541303, 25.65765475, 4.40028923, 19…
$ x_19 <dbl> 8.8461426, 12.4465517, 7.2947844, 21.1447000, 2.1949018, 13.48330…
$ x_20 <dbl> 2.89540058, 5.48058724, 6.98881342, -0.09682534, 15.03106832, 16.…
$ y <dbl> -42.86481, 46.87184, 50.14464, -119.30716, 38.10710, 90.32426, 44…Set up a tibble to track model performance in train and test
Code
error_ex2 <- tibble(model = character(), rmse_trn = numeric(), rmse_test = numeric()) |>
glimpse()Rows: 0
Columns: 3
$ model <chr>
$ rmse_trn <dbl>
$ rmse_test <dbl> 6.8.1 Fit a standard (OLS) linear regression
Fit and evaluate the linear model
Code
fit_lm_2 <-
linear_reg() |>
set_engine("lm") |>
fit(y ~ ., data = data_trn_2)
fit_lm_2 |>
tidy() |>
print(n = 21)# A tibble: 21 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -14.0 10.8 -1.30 0.198
2 x_1 2.93 1.35 2.17 0.0330
3 x_2 -0.800 1.33 -0.602 0.549
4 x_3 1.24 1.62 0.762 0.448
5 x_4 1.20 1.46 0.821 0.414
6 x_5 2.31 1.44 1.60 0.114
7 x_6 0.235 1.57 0.149 0.882
8 x_7 1.63 1.46 1.12 0.268
9 x_8 -0.548 1.33 -0.413 0.681
10 x_9 -1.19 1.38 -0.863 0.391
11 x_10 -0.187 1.67 -0.112 0.911
12 x_11 -2.19 1.36 -1.61 0.112
13 x_12 0.725 1.43 0.508 0.613
14 x_13 3.73 1.41 2.65 0.00983
15 x_14 -0.183 1.40 -0.131 0.896
16 x_15 -0.163 1.32 -0.123 0.902
17 x_16 -4.54 1.42 -3.20 0.00199
18 x_17 1.81 1.24 1.46 0.149
19 x_18 -1.19 1.31 -0.909 0.366
20 x_19 0.421 1.33 0.317 0.752
21 x_20 -0.0841 1.36 -0.0617 0.951 Irreducible error was set by y_error (100)
- Very overfit to train
- Very poor performance in test
Code
(error_ex2 <- error_ex2 |>
bind_rows(tibble(model = "linear model",
rmse_trn = rmse_vec(truth = data_trn_2$y,
estimate = predict(fit_lm_2,
data_trn_2)$.pred),
rmse_test = rmse_vec(truth = data_test_2$y,
estimate = predict(fit_lm_2,
data_test_2)$.pred))))# A tibble: 1 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 83.4 117.6.8.2 Fit LASSO
For all glmnet algorithms, set up:
- Recipe
- Feature matrices
- Bootstraps for model configuration selection (tuning)
Code
rec_2 <- recipe(y ~ ., data = data_trn_2) |>
step_normalize(all_predictors())
rec_prep_2 <- rec_2 |>
prep(data_trn_2)
feat_trn_2 <- rec_prep_2 |>
bake(NULL)
feat_test_2 <- rec_prep_2 |>
bake(data_test_2)
set.seed(20140102)
splits_boot_2 <- data_trn_2 |>
bootstraps(times = 100, strata = "y") Tune \(\lambda\) for LASSO
- We can use sample penalty grids from earlier example because sample size and number of features hasnt changed so likely still good
Code
fits_lasso_2 <- xfun::cache_rds(
expr = {
linear_reg(penalty = tune(),
mixture = 1) |>
set_engine("glmnet") |>
tune_grid(preprocessor = rec_2,
resamples = splits_boot_2,
grid = grid_lasso,
metrics = metric_set(rmse))
},
rerun = rerun_setting,
dir = "cache/006/",
file = "fits_lasso_2")Plot hyperparameters
Code
plot_hyperparameters(fits_lasso_2, hp1 = "penalty", metric = "rmse")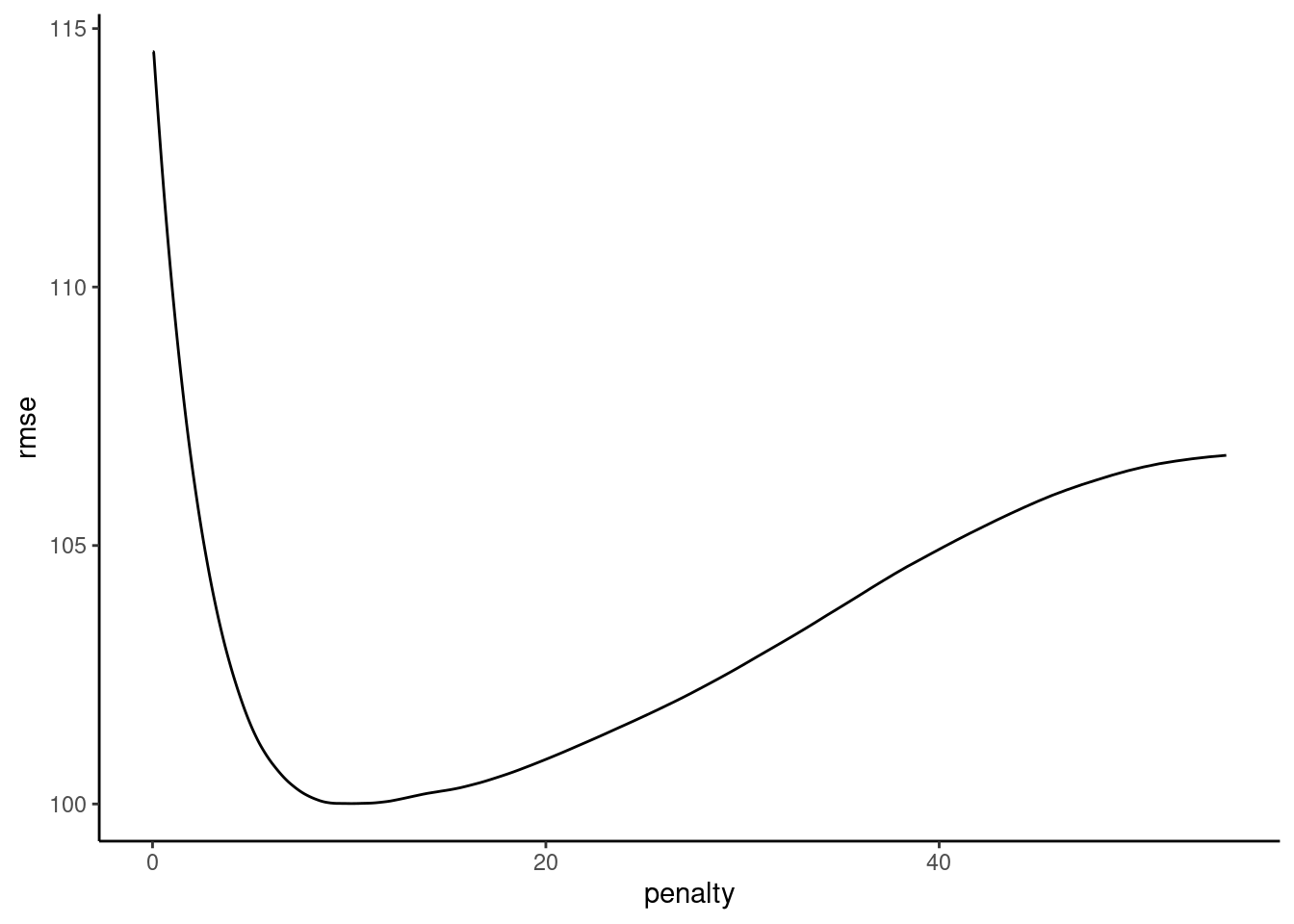
Fit best LASSO to full training set
- Notice the many \(\beta\) = 0
- It did set some of the “good” features to 0 as well
Code
fit_lasso_2 <-
linear_reg(penalty = select_best(fits_lasso_2, metric = "rmse")$penalty,
mixture = 1) |>
set_engine("glmnet") |>
fit(y ~ ., data = feat_trn_2)
fit_lasso_2 |>
tidy() |>
print(n = 21)# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) 2.06 10.1
2 x_1 19.3 10.1
3 x_2 0 10.1
4 x_3 1.16 10.1
5 x_4 9.38 10.1
6 x_5 10.9 10.1
7 x_6 0 10.1
8 x_7 9.03 10.1
9 x_8 0 10.1
10 x_9 0 10.1
11 x_10 0 10.1
12 x_11 0 10.1
13 x_12 0 10.1
14 x_13 5.48 10.1
15 x_14 0 10.1
16 x_15 0 10.1
17 x_16 -15.1 10.1
18 x_17 0 10.1
19 x_18 0 10.1
20 x_19 0 10.1
21 x_20 0 10.1Irreducible error was set by y_error (100)
- Somewhat overfit to train
- Good in val
Code
(error_ex2 <- error_ex2 |>
bind_rows(tibble(model = "LASSO model",
rmse_trn = rmse_vec(truth = feat_trn_2$y,
estimate = predict(fit_lasso_2,
feat_trn_2)$.pred),
rmse_test = rmse_vec(truth = feat_test_2$y,
estimate = predict(fit_lasso_2,
feat_test_2)$.pred))))# A tibble: 2 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 83.4 117.
2 LASSO model 91.1 102.6.8.3 Fit Ridge
Tune \(\lambda\) for Ridge
- can use ridge penalty grid from example 1
Code
fits_ridge_2 <- xfun::cache_rds(
expr = {
linear_reg(penalty = tune(),
mixture = 0) |>
set_engine("glmnet") |>
tune_grid(preprocessor = rec_2,
resamples = splits_boot_2,
grid = grid_ridge,
metrics = metric_set(rmse))
},
rerun = rerun_setting,
dir = "cache/006/",
file = "fits_ridge_2")Plot hyperparameters
Code
plot_hyperparameters(fits_ridge_2, hp1 = "penalty", metric = "rmse")
Fit best Ridge to full training set
- Notice no \(\beta\) = 0
Code
fit_ridge_2 <-
linear_reg(penalty = select_best(fits_ridge_2, metric = "rmse")$penalty,
mixture = 0) |>
set_engine("glmnet") |>
fit(y ~ ., data = feat_trn_2)
fit_ridge_2 |>
tidy() |>
print(n = 21)# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) 2.06 176.
2 x_1 9.91 176.
3 x_2 1.05 176.
4 x_3 6.11 176.
5 x_4 6.83 176.
6 x_5 7.64 176.
7 x_6 2.32 176.
8 x_7 6.76 176.
9 x_8 2.31 176.
10 x_9 0.716 176.
11 x_10 3.31 176.
12 x_11 -2.86 176.
13 x_12 -0.572 176.
14 x_13 5.93 176.
15 x_14 -1.05 176.
16 x_15 -1.75 176.
17 x_16 -8.79 176.
18 x_17 2.85 176.
19 x_18 -2.80 176.
20 x_19 -0.740 176.
21 x_20 0.362 176.Irreducible error was set by y_error (100)
- Somewhat overfit to train
- Still slightly better than LASSO in test (but maybe equivalent?)
Code
(error_ex2 <- error_ex2 |>
bind_rows(tibble(model = "Ridge model",
rmse_trn = rmse_vec(truth = feat_trn_2$y,
estimate = predict(fit_ridge_2,
feat_trn_2)$.pred),
rmse_test = rmse_vec(truth = feat_test_2$y,
estimate = predict(fit_ridge_2,
feat_test_2)$.pred))))# A tibble: 3 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 83.4 117.
2 LASSO model 91.1 102.
3 Ridge model 92.5 101.6.8.4 Fit Complete glmnet
Tune \(\lambda\) and \(\alpha\) for glmnet
Code
fits_glmnet_2 <- xfun::cache_rds(
expr = {
linear_reg(penalty = tune(),
mixture = tune()) |>
set_engine("glmnet") |>
tune_grid(preprocessor = rec_2,
resamples = splits_boot_2,
grid = grid_glmnet,
metrics = metric_set(rmse))
},
rerun = rerun_setting,
dir = "cache/006/",
file = "fits_glmnet_2")Plot hyperparameters
Code
plot_hyperparameters(fits_glmnet_2, hp1 = "penalty", hp2 = "mixture", metric = "rmse")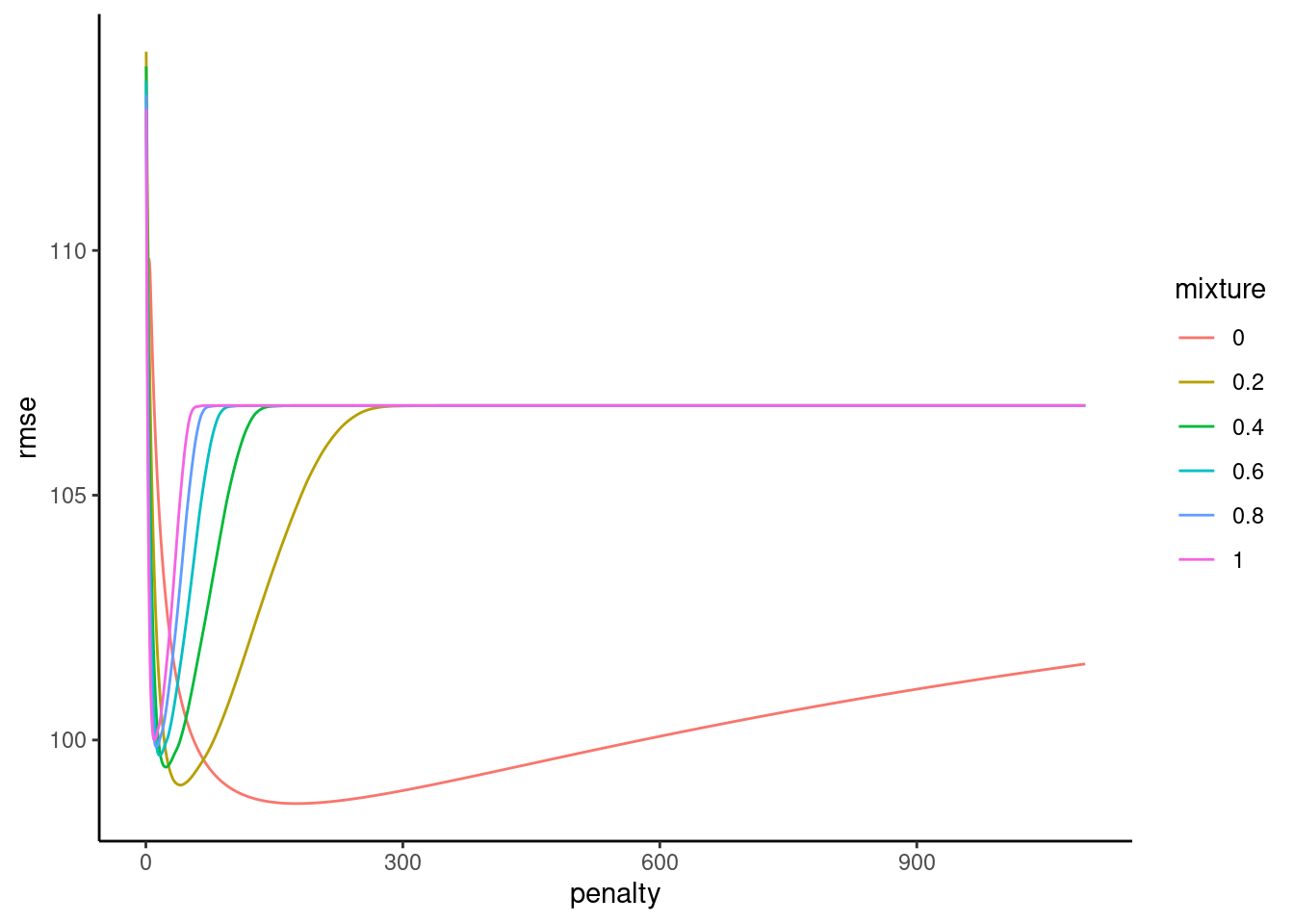
Fit best glmnet in full train set
- Still Ridge (but won’t always be)
Code
select_best(fits_glmnet_2, metric = "rmse")# A tibble: 1 × 3
penalty mixture .config
<dbl> <dbl> <chr>
1 176. 0 Preprocessor1_Model0386Code
fit_glmnet_2 <-
linear_reg(penalty = select_best(fits_glmnet_2, metric = "rmse")$penalty,
mixture = select_best(fits_glmnet_2, metric = "rmse")$mixture) |>
set_engine("glmnet") |>
fit(y ~ ., data = feat_trn_2)
fit_glmnet_2 |>
tidy() |>
print(n = 21)# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) 2.06 176.
2 x_1 9.91 176.
3 x_2 1.05 176.
4 x_3 6.11 176.
5 x_4 6.83 176.
6 x_5 7.64 176.
7 x_6 2.32 176.
8 x_7 6.76 176.
9 x_8 2.31 176.
10 x_9 0.716 176.
11 x_10 3.31 176.
12 x_11 -2.86 176.
13 x_12 -0.572 176.
14 x_13 5.93 176.
15 x_14 -1.05 176.
16 x_15 -1.75 176.
17 x_16 -8.79 176.
18 x_17 2.85 176.
19 x_18 -2.80 176.
20 x_19 -0.740 176.
21 x_20 0.362 176.Irreducible error was set by y_error (100)
- Somewhat overfit to train
- Still not bad in validate
Code
(error_ex2 <- error_ex2 |>
bind_rows(tibble(model = "glmnet model",
rmse_trn = rmse_vec(truth = feat_trn_2$y,
estimate = predict(fit_glmnet_2,
feat_trn_2)$.pred),
rmse_test = rmse_vec(truth = feat_test_2$y,
estimate = predict(fit_glmnet_2,
feat_test_2)$.pred))))# A tibble: 4 × 3
model rmse_trn rmse_test
<chr> <dbl> <dbl>
1 linear model 83.4 117.
2 LASSO model 91.1 102.
3 Ridge model 92.5 101.
4 glmnet model 92.5 101.6.9 LASSO for Feature (e.g., Covariate) Selection?
Lets consider a typical explanatory setting in Psychology
- A focal dichotomous IV (your experimental manipulation)
- A number of covariates (some good, some bad)
- A quantitative outcome (y)
- Covariates are uncorrelated with IV b/c IV is manipulated
Let’s pretend the previous 20 xs were your covariates
What are your options to test iv prior to this course?
You want to use covariates to increase power
BUT you don’t know which covariates to use
You might use all of them
Or you might use none of them (a clear lost opportunity)
Or you might hack it by using those increase your focal IV effect (very bad!)
NOW, We might use the feature selection characteristics for LASSO to select which covariates are included
There are two possibilities that occur to me
- Use LASSO to build best DGP for a covariates only model
- Could be more conservative (fewer covariates) by using within 1 SE of best performance but less flexible (i.e., will set more parameter estimates to 0)
- Follow up with a linear model (using \(lm\)), regressing y on \(iv\) and covariates from LASSO that are non-zero
Code
fit_lasso_2 |>
tidy() |>
print(n = 21)# A tibble: 21 × 3
term estimate penalty
<chr> <dbl> <dbl>
1 (Intercept) 2.06 10.1
2 x_1 19.3 10.1
3 x_2 0 10.1
4 x_3 1.16 10.1
5 x_4 9.38 10.1
6 x_5 10.9 10.1
7 x_6 0 10.1
8 x_7 9.03 10.1
9 x_8 0 10.1
10 x_9 0 10.1
11 x_10 0 10.1
12 x_11 0 10.1
13 x_12 0 10.1
14 x_13 5.48 10.1
15 x_14 0 10.1
16 x_15 0 10.1
17 x_16 -15.1 10.1
18 x_17 0 10.1
19 x_18 0 10.1
20 x_19 0 10.1
21 x_20 0 10.1- You clearly improved your best guess on covariates to include
- You will regress y on
ivand the 7 covariates with non-zero effects
- Use LASSO to build best DGP including
ivand covariates but don’t penalizeiv
- Look at
penalty.factor = rep(1, nvars)argument inglmnet() - Can fit LASSO with unbiased? estimate of
iv - Need to bootstrap for SE for
iv(next unit) - Only appropriate if IV is manipulated
Should really conduct simulation study of both of these options (vs. all and no covariates).
- I want to
- Want to do the study with me?
6.10 Ridge, LASSO, and Elastic net models for other Y distributions
These penalties can be added to the cost functions of other generalized linear models to yield regularized/penalized versions of those models as well. For example
L1 penalized (LASSO) logistic regression (w/ labels coded 0,1):
- \(\frac{1}{n}([\:\sum_{i = 1}^{n} -Y_ilog(\hat{Y_i}) - (1-Y_i)log(1-\hat{Y_i})\:]\:+\:[\:\lambda\sum_{j = 1}^{p} |\beta_j|\:]\)
For L2 penalized (Ridge) logistic regression (w/ labels coded 0,1)
- \(\frac{1}{n}([\:\sum_{i = 1}^{n} -Y_ilog(\hat{Y_i}) - (1-Y_i)log(1-\hat{Y_i})\:]\:+\:[\:\lambda\sum_{j = 1}^{p} \beta_j^{2}\:]\)
glmnet implements:
family = c("gaussian", "binomial", "poisson", "multinomial", "cox", "mgaussian")- Full range of \(\alpha\) to mix two types of penalties